Stat-Ease Blog

Categories
Hear Ye, Hear Ye: A Response Surface Method (RSM) Experiment on Sound Produces Surprising Results
A few years ago, while evaluating our training facility in Minneapolis, I came up with a fun experiment that demonstrates a great application of RSM for process optimization. It involves how sound travels to our students as a function of where they sit. The inspiration for this experiment came from a presentation by Tom Burns of Starkey Labs to our 5th European DOE User Meeting. As I reported in our September 2014 Stat-Teaser, Tom put RSM to good use for optimizing hearing aids.
Background
Classroom acoustics affect speech intelligibility and thus the quality of education. The sound intensity from a point source decays rapidly by distance according to the inverse square law. However, reflections and reverberations create variations by location for each student—some good (e.g., the Whispering Gallery at Chicago Museum of Science and Industry—a very delightful place to visit, preferably with young people in tow), but for others bad (e.g., echoing). Furthermore, it can be expected to change quite a bit from being empty versus fully occupied. (Our then-IT guy Mike, who moonlights as a sound-system tech, called these—the audience, that is—“meat baffles”.)
Sound is measured on a logarithmic scale called “decibels” (dB). The dBA adjusts for varying sensitivities of the human ear.
Frequency is another aspect of sound that must be taken into account for acoustics. According to Wikipedia, the typical adult male speaks at a fundamental frequency from 85 to 180 Hz. The range for a typical adult female is from 165 to 255 Hz.
Procedure

Stat-Ease training room at one of our old headquarters—sound test points spotted by yellow cups.
This experiment sampled sound on a 3x3 grid from left to right (L-R, coded -1 to +1) and front to back (F-B, -1 to +1)—see a picture of the training room above for location—according to a randomized RSM test plan. A quadratic model was fitted to the data, with its predictions then mapped to provide a picture of how sound travels in the classroom. The goal was to provide acoustics that deliver just enough loudness to those at the back without blasting the students sitting up front.
Using sticky notes as markers (labeled by coordinates), I laid out the grid in the Stat-Ease training room across the first 3 double-wide-table rows (4th row excluded) in two blocks:
- 2² factorial (square perimeter points) with 2 center points (CPs).
- Remainder of the 32 design (mid-points of edges) with 2 additional CPs.
I generated sound from the Online Tone Generator at 170 hertz—a frequency chosen to simulate voice at the overlap of male (lower) vs female ranges. Other settings were left at their defaults: mid-volume, sine wave. The sound was amplified by twin Dell 6-watt Harman-Kardon multimedia speakers, circa 1990s. They do not build them like this anymore 😉 These speakers reside on a counter up front—spaced about a foot apart. I measured sound intensity on the dBA scale with a GoerTek Digital Mini Sound Pressure Level Meter (~$18 via Amazon).
Results
I generated my experiment via the Response Surface tab in Design-Expert® software (this 3³ design shows up under "Miscellaneous" as Type "3-level factorial"). Via various manipulations of the layout (not too difficult), I divided the runs into the two blocks, within which I re-randomized the order. See the results tabulated below.
| Block | Run | Space Type | Coordinate (A: L-R) | Coordinate (B: F-B) | Sound (dBA) |
|---|---|---|---|---|---|
| 1 | 1 | Factorial | -1 | 1 | 70 |
| 1 | 2 | Center | 0 | 0 | 58 |
| 1 | 3 | Factorial | 1 | -1 | 73.3 |
| 1 | 4 | Factorial | 1 | 1 | 62 |
| 1 | 5 | Center | 0 | 0 | 58.3 |
| 1 | 6 | Factorial | -1 | -1 | 71.4 |
| 1 | 7 | Center | 0 | 0 | 58 |
| 2 | 8 | CentEdge | -1 | 0 | 64.5 |
| 2 | 9 | Center | 0 | 0 | 58.2 |
| 2 | 10 | CentEdge | 0 | 1 | 61.8 |
| 2 | 11 | CentEdge | 0 | -1 | 69.6 |
| 2 | 12 | Center | 0 | 0 | 57.5 |
| 2 | 13 | CentEdge | 1 | 0 | 60.5 |
Notice that the readings at the center are consistently lower than around the edge of the three-table space. So, not surprisingly, the factorial model based on block 1 exhibits significant curvature (p<0.0001). That leads to making use of the second block of runs to fill out the RSM design in order to fit the quadratic model. I was hoping things would play out like this to provide a teaching point in our DOESH class—the value of an iterative strategy of experimentation.
The 3D surface graph shown below illustrates the unexpected dampening (cancelling?) of sound at the middle of our Stat-Ease training room.
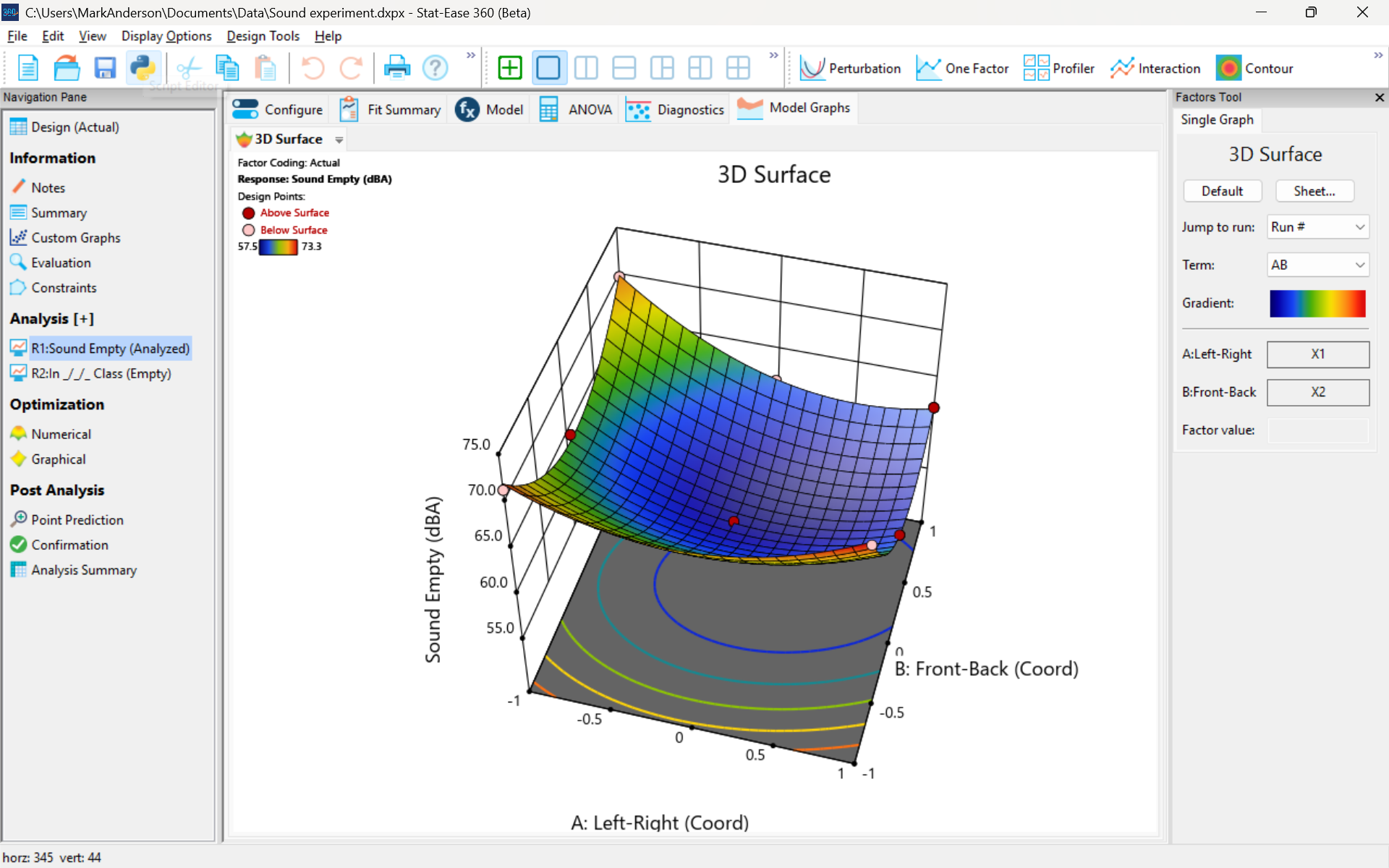
3D surface graph of sound by classroom coordinate.
Perhaps this sound ‘map’ is typical of most classrooms. I suppose that it could be counteracted by putting acoustic reflectors overhead. However, the minimum loudness of 57.4 (found via numeric optimization and flagged over the surface pictured) is very audible by my reckoning (having sat in that position when measuring the dBA). It falls within the green zone for OSHA’s decibel scale, as does the maximum of 73.6 dBA, so all is good.
What next
The results documented here came from an empty classroom. I would like to do it again with students (aka meat baffles) present. I wonder how that will affect the sound map. Of course, many other factors could be tested. For example, Rachel from our Front Office team suggested I try elevating the speakers. Another issue is the frequency of sound emitted. Furthermore, the oscillation can be varied—sine, square, triangle and sawtooth waves could be tried. Other types of speakers would surely make a big difference.
What else can you think of to experiment on for sound measurement? Let me know.
Are optimal response surface method (RSM) designs always the optimal choice?
Most people who have been exposed to design of experiment (DOE) concepts have probably heard of factorial designs—designs that target the discovery of factor and interaction effects on their process. But factorial designs are hardly the only tool in the shed. And oftentimes to properly optimize our system a more advanced response surface design (RSM) will prove to be beneficial, or even essential.
This is the case when there is “curvature” within the design space, suggesting that quadratic (or higher) order terms are needed to make valid predictions between the extreme high/low process factor settings. This gives us the opportunity to find optimal solutions that reside in the interior of the design space. If you include center points in a factorial design, you can check for non-linear behavior within the design space to see if an RSM design would be useful (1). But which RSM options should you pick?
Let’s start by introducing the Stat-Ease® software menu options for RSM designs. Once we understand the alternatives we can better understand when which might be most useful for any given situation and why optimal designs are great—when needed.
- First on the list is the central composite design (our software default)
- Next is the Box-Behnken design
- And third is something called optimal design
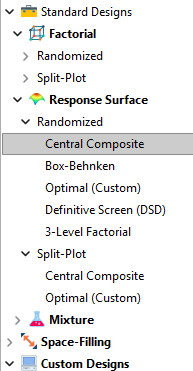
Stat-Ease software design selection options
The natural question that often pops up is this. Since optimal designs are third on our list, are we defaulting to suboptimal designs? Let’s dig in a bit deeper.
The central composite design (“CCD”) has traditionally been the workhorse of response surface methods. It has a predictable structure (5 levels for each factor). It is robust to some variations in the actual factor settings, meaning that you will still get decent quadratic model fits even if the axial runs have to be tweaked to achieve some practical values, including the extreme case when the axial points are placed at the face of the factorial “cube” making the design a 3-level study. A CCD is the design of choice when it fits the problem and generally creates predictive models that are effective throughout the design space--the factorial region of the design. Note that the quadratic predictive models generally improve when the axial points reside outside the face of the factorial cube.
When a 5-level study is not practical, for example, if we are looking at catalyst levels and the lower axial point would be zero or a negative number, we may be forced to bring the axial points to the face of the factorial cube. When this happens, Box-Behnken designs would be another standard design to consider. It is a 3-level design that is laid out slightly differently than a CCD. In general, the Box-Behnken results in a design with marginally fewer runs and is generally capable of creating very useful quadratic predictive models.
These standard designs are very effective when our experiments can be performed precisely as scripted by the design template. But this is not always the case, and when it is not we will need to apply a more novel approach to create a customized DOE.
Optimal designs are “custom” creations that come in a variety of alphabet-soup flavors—I, D, A, G, etc. The idea with optimal designs is that given your design needs and run-budget, the optimization algorithm will seek out the best choice of runs to provide you with a useful predictive model that is as effective as possible. Use of the system defaults when creating optimal designs is highly advised. Custom optimal designs often have fewer runs than the central composite option. Because they are generated by a computer algorithm, the number of levels per factor and the positioning of the points in the design space may be unique each time the design is built. This may make newcomers to optimal designs a bit uneasy. But, optimal designs fill the gap when:
- The design space is not “cuboidal”— there are constraints on the operating region that make the design space lopsided or truncated.
- There are categoric or discrete numeric factors to deal with.
- The expected polynomial model is something other than a full quadratic.
- You are trying to augment an existing design to expand the design space or to upgrade to a higher order model.
The classic designs provide simple and robust solutions and should always be considered first when planning an experiment. However, when these designs don’t work well because of budget or practical design space constraints, don’t be afraid to go “outside the box” and explore your other options. The goal is to choose a design that fits the problem!
Acknowledgement: This post is an update of an article by Shari Kraber on “Modern Alternatives to Traditional Designs Modern Alternatives to Traditional Designs" published in the April 2011 STATeaser.
(1) See Shari Kraber’s blog post, “"Energize Two-Level Factorials - Add Center Points!” from August. 23, 2018 for additional insights.
January Publication Roundup
Here's the latest Publication Roundup! In these monthly posts, we'll feature recent papers that cited Design-Expert® or Stat-Ease® 360 software. Please submit your paper to us if you haven't seen it featured yet!
Featured Article
Quantification of Menthol by Chromatography Applying Analytical Quality by Design
Chromatographia, Published: 17 January 2026
Authors: Santiago Puentes, Julian Puentes, Ronald Andrés Jiménez & Emerson León Ávila
Mark's comments: Well done deploying the Ishikawa (fishbone) diagram to consider all the factors that might affect the analytical method. This is a great application of a multifactor approach to achieve quality by design.
Be sure to check out this important study, and the other research listed below!
More new publications from January
- UHPLC Method Development for the Trace Level Quantification of Anastrozole and Its Process-Related Impurities Using Design of Experiments
Biomedical Chromatography, Volume 40, Issue 2 February 2026 e70279
Authors: Narasimha Rao Tadisetty, Ramesh Yanamandra, Subhalaxmi Pradhan, Gitanjali Pradhan - Combinatorial Anti-Mitotic Activity of Loratadine/5-Fluorouracil Loaded Zein Tannic Acid Nanoparticles in Breast Cancer Therapy: In silico, in vitro and Cell Studies
International Journal of Nanomedicine, 2026; 21:1-27
Authors: Mohamed Hamdi, Moawia M Al-Tabakha, Isra H Ali, Islam A Khalil - Synergistic effects and optimization of palm oil fuel ash and jute fiber in sustainable concrete
Scientific Reports volume 16, Article number: 259 (2026)
Authors: Muhammad Umer, Nawab Sameer Zada, Paul O. Awoyera, Muhammad Basit Khan, Wisal Ahmed, Olaolu George Fadugba - Harnessing sawdust for clean energy: production and optimization of bioethanol in Nigeria
MOJ Ecology & Environmental Sciences, 2026; 11(1):5‒11.
Authors: Ifeoma Juliet Opara, Eno-obong Sunday Nicholas, Ezekiel Adi Siman - Antibiotic-phytochemical combinations against Enterococcus faecalis: a therapeutic strategy optimized using response surface methodology
Antonie van Leeuwenhoek, 119, 41 (2026)
Authors: Monikankana Dasgupta, Alakesh Maity, Ranojit Kumar Sarker, Payel Paul, Poulomi Chakraborty, Sarita Sarkar, Ritwik Roy, Moumita Malik, Sharmistha Das & Prosun Tribedi - Breakthrough RP-HPLC strategy for synchronous analysis of pyridine and its degradation products in powder for injection using quality metrics
Scientific Reports volume 16, Article number: 1344 (2026)
Authors: Asma S. Al‐Wasidi, Noha S. katamesh, Fahad M. Alminderej, Sayed M. Saleh, Hoda A. Ahmed, Mahmoud A. Mohamed
December Publication Roundup
Here's the latest Publication Roundup! In these monthly posts, we'll feature recent papers that cited Design-Expert® or Stat-Ease® 360 software. Please submit your paper to us if you haven't seen it featured yet!
Featured Article
Sustainable protection for mild steel (S235): Anti-corrosion effectiveness of natural Paraberlinia bifoliolata barks extracts in HCl 1 M
Hybrid Advances, Volume 11, December 2025, 100526
Authors: Liliane Nga, Benoit Ndiwe, Jean Jalin Eyinga Biwolé, Armand Zébazé Ndongmo, Achille Desiré Omgba Béténé, Yvan Sandy Nké Ayinda, Joseph Zobo Mfomo, Cesar Segovia, Antonio Pizzi, Achille Bernard Biwolé
Mark's comments: I like this for its application of response surface methods to thoroughly explore three process factors for optimization of a 'green' corrosion inhibitor. They then provide a scientific explanation of its "remarkable effectiveness."
Be sure to check out this important study, and the other research listed below!
More new publications from December
- Sustainable synthesis of Mangenese cobalt oxide nanocomposite on natural clay and optimization using response surface methodology for ciprofloxacin degradation via peroxymonosulfate activation
Applied Surface Science, Volume 712, 7 December 2025, 164136
Authors: Amira Hrichi, Nesrine Abderrahim, Hédi Ben Amor, Marta Pazos, Maria Angeles Sanromán - Optimization of fermentation conditions for lactic acid production by Lactiplantibacillus plantarum OM510300 using plantain peduncles as substrate
Scientific African, Volume 30, December 2025, e02998
Authors: Oluwafemi Adebayo Oyewole, Japhet Gaius Yakubu, Nofisat Olaide Oyedokun, Konjerimam Ishaku Chimbekujwo, Priscila Yetu Tsado, Abdullah Albaqami - QbD-Based HPLC Method Development for Trace-Level Detection of Genotoxic 3-Methylbenzyl Chloride in Meclizine HCl Formulations
Biomedical Chromatography, Volume 39, Issue 12, December 2025, e70238
Authors: Naga Kranthi Kumar Chintalapudi, Naresh Podila, Vijay Kumar Chollety - Multi-objective intelligent optimization design method for mix proportions of hydraulic asphalt concrete facings
Ain Shams Engineering Journal, Volume 16, Issue 12, December 2025, 103781
Hanye Xiong, Zhenzhong Shen, Yiqing Sun, Yaxin Feng, Hongwei Zhang - Sustainable pretreatment and adsorption of chemical oxygen demand from car wash wastewater using Noug sawdust activated carbon Scientific Reports volume 15, Article number: 42464 (2025)
Authors: Getasew Yirdaw, Abraham Teym, Wolde Melese Ayele, Mengesha Genet, Ahmed Fentaw Ahmed, Assefa Andargie Kassa, Tilahun Degu Tsega, Chalachew Abiyu Ayalew, Getaneh Atikilt Yemata, Tesfaneh Shimels, Rahel Mulatie Anteneh, Abathun Temesgen, Gashaw Melkie Bayeh, Almaw Genet Yeshiwas, Habitamu Mekonen, Berhanu Abebaw Mekonnen, Meron Asmamaw Alemayehu, Sintayehu Simie Tsega, Zeamanuel Anteneh Yigzaw, Amare Genetu Ejigu, Wondimnew Desalegn Addis, Birhanemaskal Malkamu, Kalaab Esubalew Sharew, Daniel Adane, Chalachew Yenew - Ternary phase optimized indomethacin nanoemulsion hydrogel for sustained topical delivery and improved biological efficacy
Scientific Reports volume 15, Article number: 43322 (2025)
Authors: K. R. Nithin, G. M. Pallavi, K. S. Srikruthi, Kasim Sakran Abass, Nimbagal Raghavendra Naveen - Numerical and experimental investigation of CI engine parameters using palm biodiesel with diesel blends
Scientific Reports volume 15, Article number: 43399 (2025)
Authors: B. Musthafa, M. Prabhahar - Development a practical method for calculation of the block volume and block surface in a fractured rock mass
Scientific Reports volume 15, Article number: 44068 (2025)
Authors: Alireza Shahbazi, Ali Saeidi, Alain Rouleau, Romain Chesnaux - Biofabrication, statistical optimization, and characterization of collagen nanoparticles synthesized via Streptomyces cell-free system for cancer therapy
Scientific Reports volume 15, Article number: 43835 (2025)
Authors: Noura El-Ahmady El-Naggar, Shaimaa Elyamny, Ahmad G. Shitifa, Asmaa Atallah El-Sawah
November Publication Roundup
Here's the latest Publication Roundup! In these monthly posts, we'll feature recent papers that cited Design-Expert® or Stat-Ease® 360 software. Please submit your paper to us if you haven't seen it featured yet!
Featured Article
Lipid nanocapsule-chitosan and iota-carrageenan hydrogel composite for sustained hydrophobic drug delivery
Scientific Reports volume 15, Article number: 42349 (November 27, 2025)
Authors: Grady K. Mukubwa, Justin B. Safari, Zikhona N. Tetana, Caroline N. Jones, Roderick B. Walker, Rui W. M. Krause
Mark's comments: This is an outstanding application of mixture design for optimal formulation of a novel composite system for enhancing oral delivery of hydrophilic antiviral drugs--a very worthy cause.
Be sure to check out this important study, and the other research listed below!
More new publications from November
- Design and optimization of lamivudine-loaded nanostructured lipid carriers: Improved lipid screening for effective drug delivery
Journal of Drug Delivery Science and Technology, Volume 113, November 2025, 107349
Authors: Hüsniye Hande Aydın, Esra Karataş, Zeynep Şenyiğit, Hatice Yeşim Karasulu - Improving the efficacy and targeting of carvedilol for the management of diabetes-accelerated atherosclerosis: An in vitro and in vivo assessment
European Journal of Pharmacology, Volume 1006, 5 November 2025, 178134
Authors: Marwa M. Nagib, Ala Hussain Haider, Amr Gamal Fouad, Sherif Faysal Abdelfattah Khalil, Amany Belal, Fahad H. Baali, Nisreen Khalid Aref Albezrah, Alaa Ismail, Fatma I. Abo El-Ela - Evaluating the bioavailability and therapeutic efficacy of nintedanib-loaded novasomes as a therapy for non-small cell lung cancer
Journal of Pharmaceutical Sciences, Volume 114, Issue 11, 103998, November 2025
Authors: Tamer M. Mahmoud, Amr Gamal Fouad, Amany Belal, Alaa Ismail, Fahad H. Baali, Mohammed S Alharthi, Ahmed H.E. Hassan, Eun Joo Roh, Alaa S. Tulbah, Fatma I. Abo El-Ela - Process optimization and quality assessment of redistilled Ethiopian traditional spirit (Areke): ethanol yield and zinc contamination control
Scientific Reports volume 15, Article number: 39187 (November 10, 2025)
Authors: Estifanos Kassahun, Abdiwak Tamene, Yobsen Tadesse, Bethlehem Semagn, Addisu Sewunet, Shiferaw Ayalneh, Solomon Tibebu - Box–Behnken design approach for optimizing the removal of non-steroidal anti-inflammatory drugs from environmental water samples using magnetic nanocomposite
Scientific Reports volume 15, Article number: 40223 (November 17, 2025)
Authors: Chuanyong Yan, Ying Zhang, Li Feng - Influence of process parameters on single-cell oil production by Cutaneotrichosporon oleaginosus using response surface methodology
Biotechnology for Biofuels and Bioproducts, Volume 18, article number 115 (19 November 2025)
Authors: Max Schneider, Felix Melcher, Robert Fimmen, Johannes Mertens, Daniel Garbe, Michael Paper, Marion Ringel, Thomas Brück - Rheology, strength and durability performance of bentonite-enhanced high-performance concrete
Scientific Reports volume 15, Article number: 40487 (November 18, 2025)
Authors: M. Achyutha Kumar Reddy, Veerendrakumar C. Khed, Naga Chaitanya Kavuri - Surface-engineered hyaluronic acid-coated lyotropic liquid crystalline nanoparticles for CD44-targeting of 3-Acetyl-11-keto-β-boswellic acid in rheumatoid arthritis treatment
Journal of Nanobiotechnology, Volume 23, article number 725, (20 November 2025)
Authors: Sakshi Priya, Vagesh Verma, Aniruddha Roy, Gautam Singhvi - Synergistic enzyme action boosts phenolic compounds in flaxseed during germination using a two-level factorial design
Scientific Reports volume 15, Article number: 40384 (November 18, 2025)
Authors: Amal Z. Barakat, Azza M. Abdel-Aty, Hala A. Salah, Roqaya I. Bassuiny, Saleh A. Mohamed
