Stat-Ease Blog

Categories
Know the SCOR for a winning strategy of experiments
Observing process improvement teams at Imperial Chemical Industries in the late 1940s George Box, the prime mover for response surface methods (RSM), realized that as a practical matter, statistical plans for experimentation must be very flexible and allow for a series of iterations. Box and other industrial statisticians continued to hone the strategy of experimentation to the point where it became standard practice for stats-savvy industrial researchers.
Via their Management and Technology Center (sadly, now defunct), Du Pont then trained legions of engineers, scientists, and quality professionals on a “Strategy of Experimentation” called “SCO” for its sequence of screening, characterization and optimization. This now-proven SCO strategy of experimentation, illustrated in the flow chart below, begins with fractional two-level designs to screen for previous unknown factors. During this initial phase, experimenters seek to discover the vital few factors that create statistically significant effects of practical importance for the goal of process improvement.

The ideal DOE for screening resolves main effects free of any two-factor interactions (2FI’s) in broad and shallow two-level factorial design. I recommend the “resolution IV” choices color-coded yellow on our “Regular Two-Level” builder (shown below). To get a handy (pun intended) primer on resolution, watch at least the first part of this Institute of Quality and Reliability YouTube video on Fractional Factorial Designs, Confounding and Resolution Codes.
If you would like to screen more than 8 factors, choose one of our unique “Min-Run Screen” designs. However, I advise you accept the program default to add 2 runs and make the experiment less susceptible to botched runs.

Stat-Ease® 360 and Design-Expert® software conveniently color-code and label different designs.
After throwing the trivial many factors off to the side (preferably by holding them fixed or blocking them out), the experimental program enters the characterization phase (the “C”) where interactions become evident. This requires a higher-resolution of V or better (green Regular Two-Level or Min-Run Characterization), or possibly full (white) two-level factorial designs. Also, add center points at this stage so curvature can be detected.
If you encounter significant curvature (per the very informative test provided in our software), use our design tools to augment your factorial design into a central composite for response surface methods (RSM). You then enter the optimization phase (the “O”).
However, if curvature is of no concern, skip to ruggedness (the “R” that finalizes the “SCOR”) and, hopefully, confirm with a low resolution (red) two-level design or a Plackett-Burman design (found under “Miscellaneous” in the “Factorial” section). Ideally you then find that your improved process can withstand field conditions. If not, then you will need to go back up to the beginning for a do-over.
The SCOR strategy, with some modification due to the nature of mixture DOE, works equally well for developing product formulations as it does for process improvement. For background, see my October 2022 blog on Strategy of Experiments for Formulations: Try Screening First!
Stat-Ease provides all the tools and training needed to deploy the SCOR strategy of experiments. For more details, watch my January webinar on YouTube. Then to master it, attend our Modern DOE for Process Optimization workshop.
Know the SCOR for a winning strategy of experiments!
Augmenting One-Factor-at-a-Time Data to Build a DOE
I am often asked if the results from one-factor-at-a-time (OFAT) studies can be used as a basis for a designed experiment. They can! This augmentation starts by picturing how the current data is laid out, and then adding runs to fill out either a factorial or response surface design space.
One way of testing multiple factors is to choose a starting point and then change the factor level in the direction of interest (Figure 1 – green dots). This is often done one variable at a time “to keep things simple”. This data can confirm an improvement in the response when any of the factors are changed individually. However, it does not tell you if making changes to multiple factors at the same time will improve the response due to synergistic interactions. With today’s complex processes, the one-factor-at-a-time experiment is likely to provide insufficient information.

Figure 1: OFAT
The experimenter can augment the existing data by extending a factorial box/cube from the OFAT runs and completing the design by running the corner combinations of the factor levels (Figure 2 – blue dots). When analyzing this data together, the interactions become clear, and the design space is more fully explored.

Figure 2: Fill out to factorial region
In other cases, OFAT studies may be done by taking a standard process condition as a starting point and then testing factors at new levels both lower and higher than the standard condition (see Figure 3). This data can estimate linear and nonlinear effects of changing each factor individually. Again, it cannot estimate any interactions between the factors. This means that if the process optimum is anywhere other than exactly on the lines, it cannot be predicted. Data that more fully covers the design space is required.

Figure 3: OFAT
A face-centered central composite design (CCD)—a response surface method (RSM)—has factorial (corner) points that define the region of interest (see Figure 4 – added blue dots). These points are used to estimate the linear and the interaction effects for the factors. The center point and mid points of the edges are used to estimate nonlinear (squared) terms.

Figure 4: Face-Centered CCD
If an experimenter has completed the OFAT portion of the design, they can augment the existing data by adding the corner points and then analyzing as a full response surface design. This set of data can now estimate up to the full quadratic polynomial. There will likely be extra points from the original OFAT runs, which although not needed for model estimation, do help reduce the standard error of the predictions.
Running a statistically designed experiment from the start will reduce the overall experimental resources. But it is good to recognize that existing data can be augmented to gain valuable insights!
Learn more about design augmentation at the January webinar: The Art of Augmentation – Adding Runs to Existing Designs.
Wrap-Up: Thanks for a great 2022 Online DOE Summit!
Thank you to our presenters and all the attendees who showed up to our 2022 Online DOE Summit! We're proud to host this annual, premier DOE conference to help connect practitioners of design of experiments and spread best practices & tips throughout the global research community. Nearly 300 scientists from around the world were able to make it to the live sessions, and many more will be able to view the recordings on the Stat-Ease YouTube channel in the coming months.
Due to a scheduling conflict, we had to move Martin Bezener's talk on "The Latest and Greatest in Design-Expert and Stat-Ease 360." This presentation will provide a briefing on the major innovations now available with our advanced software product, Stat-Ease 360, and a bit of what's in store for the future. Attend the whole talk to be entered into a drawing for a free copy of the book DOE Simplified: Practical Tools for Effective Experimentation, 3rd Edition. New date and time: Wednesday, October 12, 2022 at 10 am US Central time.
Even if you registered for the Summit already, you'll need to register for the new time on October 12. Click this link to head to the registration page. If you are not able to attend the live session, go to the Stat-Ease YouTube channel for the recording.

Want to be notified about our upcoming live webinars throughout the year, or about other educational opportunities? Think you'll be ready to speak on your own DOE experiences next year? Sign up for our mailing list! We send emails every month to let you know what's happening at Stat-Ease. If you just want the highlights, sign up for the DOE FAQ Alert to receive a newsletter from Engineering Consultant Mark Anderson every other month.
Thank you again for helping to make the 2022 Online DOE Summit a huge success, and we'll see you again in 2023!
Randomization Done Right
Randomization is essential for success with planned experimentation (DOE) to protect factor effects against bias by lurking variables. For example, consider the 8-run, two-level factorial design shown in Table 1. It lays out the low (−) and high (+) coded levels of each factor in standard, not random, order. Notice that factor C changes level only once throughout the experiment—first being set at the low (minus) level for four runs, followed by the remaining four runs set at the high (plus) level. Now, let’s say that the humidity in the room increases throughout the day—affecting the measured response. Since the DOE runs are not randomized, the change in humidity biases the calculated effect of the non-randomized factor C. Therefore, the effect of factor C includes the humidity change – it is no longer purely due to the change from low to high. This will cause analysis problems!

Table 1: Standard order of 8-run design
Randomization itself presents some problems. For example, one possible random order is the classic standard layout, which, as you now know, does not protect against time-related effects. If this unlikely pattern, or other non-desirable patterns are seen, then you should re-randomize the runs to reduce the possibility of bias from lurking variables.
Randomizing center points or other replicates
Replicates, such as center points, are used to collect information on the pure error of the system. To optimize the validity of this information, center points should be spaced out over the experimental run order. Random order may inadvertently place replicates in sequential order. This requires manual intervention by the researcher to break up or separate the repeated runs so that each run is completed independently of the matching run.
In both Design-Expert® software and Stat-Ease 360 you can re-randomize by right-clicking on the Run column header and selecting Randomize, as shown in Figure 1. You can also simply edit the Run order and swap two runs by changing the run numbers manually. This is often the easiest method when you want to separate center points, for example.

Figure 1: Right-click to Randomize
When Randomization Doesn’t Work
While randomization is ideal statistically, sometimes it is cumbersome in practice. For instance, temperature can take a very long time to change, so completely randomizing the runs may cause the experiment to go way beyond the time budget. In this case, researchers look for ways to reduce the complete randomization of the design.
I want to highlight a common DOE mistake. An incorrect way to restrict the randomization is to use blocks. Blocking is a statistical technique that groups the experimental runs to eliminate a potential source of variation from the data analysis. A common blocking factor is “day”, setting the block groups to eliminate day-to-day variation. Although this is a form of restricting randomization, if you block on an experimental factor like temperature, then statistically the block (temperature) effect will be removed from the analysis. Any interaction effect with that block will also be removed. The removal of this key effect very likely destroys the entire analysis! Blocking is not a useful method for restricting the randomization of a factor that is being studied in the experiment. For more information on why you would block, see “Blocking: Mowing the Grass in Your Experimental Backyard”.
If factor changes need to be restricted (not fully randomized), then building a split-plot design is the best way to go. A split-plot design takes into account the hard-to-change versus easy-to-change factors in a restricted randomization test plan. Perfect! The associated analysis properly assesses the differences in variation between these two groups of factors and provides the correct effect evaluation. The statistical analysis is a bit more complex, but good DOE software will handle it easily. Split-plot designs are a more complex topic, but commonly used in today’s experimental practices. Learn more about split-plot designs in this YouTube video: Split Plot Pros and Cons – Dealing with a Hard-to-Change Factor.
Wrapping up
Randomization is essential for valid and unbiased factor effect calculations, which is central to effective design of experiments analysis. It is up to the experimenter to ensure that the randomization of the experimental runs meets the DOE goals. Manual intervention may be required to separate any replicated points, such as center points. If complete randomization is not possible from a practical standpoint, build a split-plot design that statistically accounts for those restrictions.
Blocking: Mowing the Grass in Your Experimental Backyard
One challenge of running experiments is controlling the variation from process, sampling and measurement. Blocking is a statistical tool used to remove the variation coming from uncontrolled variables that are not part of the experiment. When the noise is reduced, the primary factor effects are estimated more easily, which allows the system to be modeled more precisely.
For example, an experiment may contain too many runs to be completed in just one day. However, the process may not operate identically from one day to the next, causing an unknown amount of variation to be added to the experimental data. By blocking on the days, the day-to-day variation is removed from the data before the factor effects are calculated. Other typical blocking variables are raw material batches (lots), multiple “identical” machines or test equipment, people doing the testing, etc. In each case the blocking variable is simply a resource required to run the experiment-- not a factor of interest.
Blocking is the process of statistically splitting the runs into smaller groups. The researcher might assume that arranging runs into groups randomly is ideal - we all learn that random order is best! However, this is not true when the goal is to statistically assess the variation between groups of runs, and then calculate clean factor effects. Design-Expert® software splits the runs into groups using statistical properties such as orthogonality and aliasing. For example, a two-level factorial design will be split into blocks using the same optimal technique used for creating fractional factorials. The design is broken into parts by using the coded pattern of the high-order interactions. If there are 5 factors, the ABCDE term can be used. All the runs with “-” levels of ABCDE are put in the first block, and the runs with “+“ levels of ABCDE are put in the second block. Similarly, response surface designs are also blocked statistically so that the factor effects can be estimated as cleanly as possible.
Blocks are not “free”. One degree of freedom (df) is used for each additional block. If there are no replicates in the design, such as a standard factorial design, then a model term may be sacrificed to filter out block-by-block variation. Usually these are high-order interactions, making the “cost” minimal.
After the experiment is completed, the data analysis begins. The first line in the analysis of variance (ANOVA) will be a Block sum of squares. This is the amount of variation in the data that is due to the block-to-block differences. This noise is removed from the total sum of squares before any other effects are calculated. Note: Since blocking is a restriction on the randomization of the runs, this violates one of the ANOVA assumptions (independent residuals) and no F-test for statistical significance is done. Once the block variation is removed, the model terms can be tested against a smaller residual error. This allows factor effects to stand out more, strengthening their statistical significance.
Example showing the advantage of blocking:
In this example, a 16-blend mixture experiment aimed at fitting a special-cubic model is completed over 2 days. The formulators expect appreciable day-to-day variation. Therefore, they build a 16-run blocked design (8-runs per day). Here is the ANOVA:

The adjusted R² = 0.8884 and the predicted R² = 0.7425. Due to the blocking, the day-to-day variation (sum of squares of 20.48) is removed. This increases the sensitivity of the remaining tests, resulting in an outstanding predictive model!
What if these formulators had not thought of blocking and, instead, simply, run the experiment in a completely randomized order over two days? The ANOVA (again for the designed-for special-cubic mixture model) now looks like this:
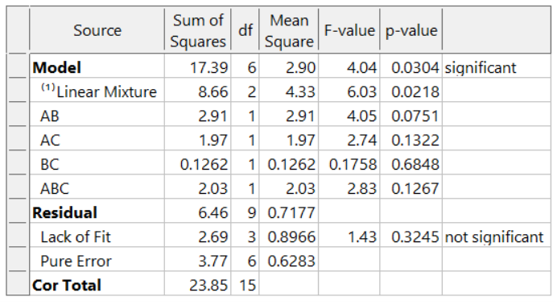
The model is greatly degraded, with adjusted R² = 0.5487, and predicted R² = 0.0819 and includes many insignificant terms. While the blocked model shown above explains 74% of the variation in predictions (the predicted R-Square), the unblocked model explains only 8% of the variation in predictions, leaving 92% unexplained. Due to the randomization of the runs, the day-to-day variation pollutes all the effects, thus reducing the prediction ability of the model.
Conclusion:
Blocks are like an insurance policy – they cost a little, and often aren’t required. However, when they are needed (block differences large) they can be immensely helpful for sorting out the real effects and making better predictions. Now that you know about blocking, consider whether it is needed to make the most of your next experiment.
Blocking FAQs:
How many runs should be in a block?
My rule-of-thumb is that a block should have at least 4 runs. If the block size is smaller, then don’t use blocking. In that case, the variable is simply another source of variation in the process.
Can I block a design after I’ve run it?
You cannot statistically add blocks to a design after it is completed. This must be planned into the design at the building stage. However, Design-Expert has sophisticated analysis tools and can analyze a block effect even if it was not done perfectly (added to the design after running the experiment). In this case, use Design Evaluation to check the aliasing with the blocks, watching for main effects or two-factor interactions (2FI).
Are there any assumptions being made about the blocks?
There is an assumption that the difference between the blocks is a simple linear shift in the data, and that this variable does not interact with any other variable.
I want to restrict the randomization of my factor because it is hard to change the setting with every run. Can I use blocking to do this?
No! Only block on variables that you are not studying. If you need to restrict the randomization of a factor, consider using a split-plot design.
