Stat-Ease Blog

Observing process improvement teams at Imperial Chemical Industries in the late 1940s George Box, the prime mover for response surface methods (RSM), realized that as a practical matter, statistical plans for experimentation must be very flexible and allow for a series of iterations. Box and other industrial statisticians continued to hone the strategy of experimentation to the point where it became standard practice for stats-savvy industrial researchers.

Via their Management and Technology Center (sadly, now defunct), Du Pont then trained legions of engineers, scientists, and quality professionals on a “Strategy of Experimentation” called “SCO” for its sequence of screening, characterization and optimization. This now-proven SCO strategy of experimentation, illustrated in the flow chart below, begins with fractional two-level designs to screen for previous unknown factors. During this initial phase, experimenters seek to discover the vital few factors that create statistically significant effects of practical importance for the goal of process improvement.

The ideal DOE for screening resolves main effects free of any two-factor interactions (2FI’s) in broad and shallow two-level factorial design. I recommend the “resolution IV” choices color-coded yellow on our “Regular Two-Level” builder (shown below). To get a handy (pun intended) primer on resolution, watch at least the first part of this Institute of Quality and Reliability YouTube video on Fractional Factorial Designs, Confounding and Resolution Codes.

If you would like to screen more than 8 factors, choose one of our unique “Min-Run Screen” designs. However, I advise you accept the program default to add 2 runs and make the experiment less susceptible to botched runs.

After throwing the trivial many factors off to the side (preferably by holding them fixed or blocking them out), the experimental program enters the characterization phase (the “C”) where interactions become evident. This requires a higher-resolution of V or better (green Regular Two-Level or Min-Run Characterization), or possibly full (white) two-level factorial designs. Also, add center points at this stage so curvature can be detected.

If you encounter significant curvature (per the very informative test provided in our software), use our design tools to augment your factorial design into a central composite for response surface methods (RSM). You then enter the optimization phase (the “O”).

However, if curvature is of no concern, skip to ruggedness (the “R” that finalizes the “SCOR”) and, hopefully, confirm with a low resolution (red) two-level design or a Plackett-Burman design (found under “Miscellaneous” in the “Factorial” section). Ideally you then find that your improved process can withstand field conditions. If not, then you will need to go back up to the beginning for a do-over.

The SCOR strategy, with some modification due to the nature of mixture DOE, works equally well for developing product formulations as it does for process improvement. For background, see my October 2022 blog on Strategy of Experiments for Formulations: Try Screening First!

Stat-Ease provides all the tools and training needed to deploy the SCOR strategy of experiments. For more details, watch my January webinar on YouTube. Then to master it, attend our Modern DOE for Process Optimization workshop.

Know the SCOR for a winning strategy of experiments!

Note: If you are interested in learning more, and to see these graphs in action, check out this YouTube video “Dive into Diagnostics to Discover Data Discrepancies”

The purpose of running a statistically designed experiment (DOE) is to take a strategically selected small sample of data from a larger system, and then extract a prediction equation that appropriately models the overall system. The statistical tool used to relate the independent factors to the dependent responses is analysis of variance (ANOVA). This article will lay out the key assumptions for ANOVA and how to verify them using graphical diagnostic plots.

The first assumption (and one that is often overlooked) is that the chosen model is correct. This means that the terms in the model explain the relationship between the factors and the response, and there are not too many terms (over-fitting), or too few terms (under-fitting). The adjusted R-squared and predicted R-squared values specify the amount of variation in the data that is explained by the model, and the amount of variation in predictions that is explained by the model, respectively. A lack of fit test (assuming replicates have been run) is used to assess model fit over the design space. These statistics are important but are outside the scope of this article.

The next assumptions are focused on the residuals—the difference between an actual observed value and its predicted value from the model. If the model is correct (first assumption), then the residuals should have no “signal” or information left in them. They should look like a sample of random variables and behave as such. If the assumptions are violated, then all conclusions that come from the ANOVA table, such as p-values, and calculations like R-squared values, are wrong. The assumptions for validity of the ANOVA are that the residuals:

• Are (nearly) independent,
• Have a mean = 0,
• Have a constant variance,
• Follow a well-behaved distribution (approximately normal).

Independence: since the residuals are generated based on a model (the difference between actual and predicted values) they are never completely independent. But if the DOE runs are performed in a randomized order, this reduces correlations from run to run, and independence can be nearly achieved. Restrictions on the randomization of the runs degrade the statistical validity of the ANOVA. Use a “residuals versus run order” plot to assess independence.

Mean of zero: due to the method of calculating the residuals for the ANOVA in DOE, this is given mathematically and does not have to be proven.

Constant variance: the response values will range from smaller to larger. As the response values increase, the residuals should continue to exhibit the same variance. If the variation in the residuals increases as the response increases, then this is non-constant variance. It means that you are not able to predict larger response values as precisely as smaller response values. Use a “residuals versus predicted value” graph to check for non-constant variance or other patterns.

Well-behaved (nearly normal) distribution: the residuals should be approximately normally distributed, which you can check on a normal probability plot.

A frequent misconception by researchers is to believe that the raw response data needs to be normally distributed to use ANOVA. This is wrong. The normality assumption is on the residuals, not the raw data. A response transformation such as a log may be used on non-normal data to help the residuals meet the ANOVA assumptions.

Repeating a statement from above, if the assumptions are violated, then all conclusions that come from the ANOVA table, such as p-values, and calculations like R-squared values, are wrong, at least to some degree. Small deviations from the desired assumptions are likely to have small effects on the final predictions of the model, while large ones may have very detrimental effects. Every DOE needs to be verified with confirmation runs on the actual process to demonstrate that the results are reproducible.

Good luck with your experimentation!

Thank you to our presenters and all the attendees who showed up to our 2022 Online DOE Summit! We're proud to host this annual, premier DOE conference to help connect practitioners of design of experiments and spread best practices & tips throughout the global research community. Nearly 300 scientists from around the world were able to make it to the live sessions, and many more will be able to view the recordings on the Stat-Ease YouTube channel in the coming months.

Due to a scheduling conflict, we had to move Martin Bezener's talk on "The Latest and Greatest in Design-Expert and Stat-Ease 360." This presentation will provide a briefing on the major innovations now available with our advanced software product, Stat-Ease 360, and a bit of what's in store for the future. Attend the whole talk to be entered into a drawing for a free copy of the book DOE Simplified: Practical Tools for Effective Experimentation, 3rd Edition. New date and time: Wednesday, October 12, 2022 at 10 am US Central time.

Even if you registered for the Summit already, you'll need to register for the new time on October 12. Click this link to head to the registration page. If you are not able to attend the live session, go to the Stat-Ease YouTube channel for the recording.

Want to be notified about our upcoming live webinars throughout the year, or about other educational opportunities? Think you'll be ready to speak on your own DOE experiences next year? Sign up for our mailing list! We send emails every month to let you know what's happening at Stat-Ease. If you just want the highlights, sign up for the DOE FAQ Alert to receive a newsletter from Engineering Consultant Mark Anderson every other month.

Thank you again for helping to make the 2022 Online DOE Summit a huge success, and we'll see you again in 2023!

An analysis of variance (ANOVA) is often accompanied by a model-validation statistic called a lack of fit (LOF) test. A statistically significant LOF test often worries experimenters because it indicates that the model does not fit the data well. This article will provide experimenters a better understanding of this statistic and what could cause it to be significant.

The LOF formula is:

where MS = Mean Square. The numerator (“Lack of fit”) in this equation is the variation between the actual measurements and the values predicted by the model. The denominator (“Pure Error”) is the variation among any replicates. The variation between the replicates should be an estimate of the normal process variation of the system. Significant lack of fit means that the variation of the design points about their predicted values is much larger than the variation of the replicates about their mean values. Either the model doesn't predict well, or the runs replicate so well that their variance is small, or some combination of the two.

Case 1: The model doesn’t predict well

On the left side of Figure 1, a linear model is fit to the given set of points. Since the variation between the actual data and the fitted model is very large, this is likely going to result in a significant LOF test. The linear model is not a good fit to this set of data. On the right side, a quadratic model is now fit to the points and is likely to result in a non-significant LOF test. One potential solution to a significant lack of fit test is to fit a higher-order model.

Case 2: The replicates have unusually low variability

Figure 2 (left) is an illustration of a data set that had a statistically significant factorial model, including some center points with variation that is similar to the variation between other design points and their predictions. Figure 2 (right) is the same data set with the center points having extremely small variation. They are so close together that they overlap. Although the predicted factorial model fits the model points well (providing the significant model fit), the differences between the actual data points are substantially greater than the differences between the center points. This is what triggers the significant LOF statistic. The center points are fitting better than the model points. Does this significant LOF require us to declare the model unusable? That remains to be seen as discussed below.

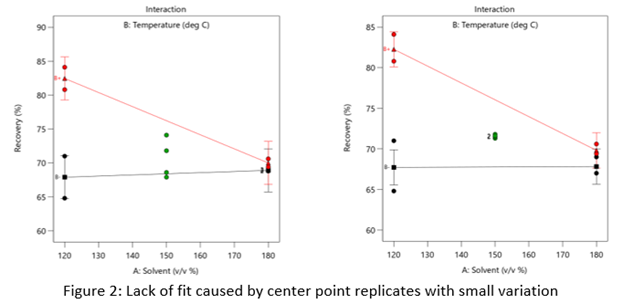
When there is significant lack of fit, check how the replicates were run— were they independent process conditions run from scratch, or were they simply replicated measurements on a single setup of that condition? Replicates that come from independent setups of the process are likely to contain more of the natural process variation. Look at the response measurements from the replicates and ask yourself if this amount of variation is similar to what you would normally expect from the process. If the “replicates" were run more like repeated measurements, it is likely that the pure error has been underestimated (making the LOF denominator artificially small). In this case, the lack of fit statistic is no longer a valid test and decisions about using the model will have to be made based on other statistical criteria.

If the replicates have been run correctly, then the significant LOF indicates that perhaps the model is not fitting all the design points well. Consider transformations (check the Box Cox diagnostic plot). Check for outliers. It may be that a higher-order model would fit the data better. In that case, the design probably needs to be augmented with more runs to estimate the additional terms.

If nothing can be done to improve the fit of the model, it may be necessary to use the model as is and then rely on confirmation runs to validate the experimental results. In this case, be alert to the possibility that the model may not be a very good predictor of the process in specific areas of the design space.

The origin of the KCV designs goes back to a mixtures short-course that I taught for Doug Montgomery at an adhesives company in Ohio. One of the topics was mixture-process variables experiments, and Doug's notes for the course contained an example using ratios of mixture proportions with the process variables. Looking at the resulting designs, I recognized that ratios did not cover the mixture design space well. Scott Kowalski was beginning his dissertation at the time. Suddenly, he had a new chapter (actually two new chapters)!

The basic idea underlying the KCV designs is to start with a true second-order model in both the mixture and process variables and then to apply the mixture constraint. The mixture constraint is subtle and can produce several models, each with a different number of terms. A fundamental assumption underlying the KCV designs is that the mixture by process variable interactions are of serious interest, especially in production. Typically, corporate R&D develops the basic formulation, often under extremely pristine conditions. Too often, R&D makes the pronouncement that "Thou shall not play with the formula." However, there are situations where production is much smoother if we can take advantage of a mixture component by process variable interaction that improves yields or minimizes a major problem. Of course, that change requires changing the formula.

Cornell (2002) is the definitive text for all things dealing with mixture experiments. It covers every possible model for every situation. However, John in his research always tended to treat the process variables as nuisance. In fact, John's intuitions on Taguchi's combined array go back to the famous fish patty experiment in his book. The fish patty experiment looked at combining three different types of fish and involved three different processing conditions. John's intuition was how to create the best formulation robust to the processing conditions, recognizing that the use of these fish patties was in a major fast-food chain. The processing conditions in actual practice typically were in the hands of teenagers who may or may not follow the protocol precisely.

John's basic instincts followed the corporate R&D-production divide. He rarely, if ever, truly worried about the mixture by process variable interactions. In addition, his first instinct always was to cross a full mixture component experiment with a full factorial experiment in the process variables. If he needed to fractionate a mixture-process experiment, he always fractionated the process variable experiment, because it primarily provided the "noise".

The basic KCV approach reversed the focus. Why can we not fractionate the mixture experiment in such a way that if a process variable is not significant, the resulting design projects down to a standard full mixture experiment? In the process, we also can see the impact of possible mixture by process variable interactions.

I still vividly remember when Scott presented the basic idea in his very first dissertation committee meeting. Of course, John Cornell was on Scott's committee. In Scott's first committee meeting, he outlined the full second-order model in both the mixture and process variables and then proceeded to apply the mixture constraint in such a way as to preserve the mixture by process variable interactions. John, who was not the biggest fan of optimal designs when a standard mixture experiment would work well, immediately jumped up and ran to the board where Scott was presenting the basic idea. John was afraid that we were proposing to use this model and apply our favorite D-optimal algorithm, which may or may not look like a standard mixture design. John and I were very good friends. I simply told him to sit down and wait a few minutes. He reluctantly did. Five minutes later, Scott presented our design strategy for the basic KCV designs, illustrating the projection properties where if a process variable was unimportant the mixture design collapsed to a standard full mixture experiment. John saw that this approach addressed his basic concerns about the blind use of an optimal design algorithm. He immediately became a convert, hence the C in KCV. He saw that we were basically crossing a good design in the process variables, which itself could be a fraction, with a clever fraction of the mixture component experiment.

John's preference to cross a mixture experiment with a process variable design meant that it was very easy to extend these designs to split-plot structures. As a result, we had two very natural chapters for Scott's dissertation. The first paper (Kowalski, Cornell, and Vining 2000) appeared in Communications in Statistics in a special issue guest edited by Norman Draper. The second paper (Kowalski, Cornell, and Vining 2002) appeared in Technometrics.

There are several benefits to the KCV design strategy. First, these designs have very nice projection properties. Of course, they were constructed specifically to achieve this goal. Second, it can significantly reduce the overall design size while still preserving the ability to estimate highly informative models. Third, unlike the approach that I taught in Ohio, the KCV designs cover the mixture experimental design space much better while still providing the equivalent information. The underlying models for both approaches are equivalent.

It has been very gratifying to see Design-Expert incorporate the KCV designs. We hope that Design-Expert users find them valuable.

References

Cornell, J.A. (2002). Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data, 3rd ed. NewYork: John Wiley and Sons.

Kowalski, S.M., Cornell, J.A., and Vining, G.G. (2000). “A New Model and Class of Designs for Mixture Experiments with Process Variables,” Communications in Statistics – Theory and Methods, 29, pp. 2255-2280.

Kowalski, S.M., Cornell, J.A., and Vining, G.G. (2002). “Split-Plot Designs and Estimation Methods for Mixture Experiments with Process Variables,” Technometrics, 44, pp. 72-79.